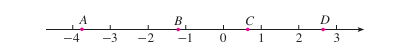更新记录
注意：仅作参考

2025-8-26

自发布以来暂未更新。

这节课，我们将更加深入地探究有理数。

1.3.1 相反数

像1和-1，321123\frac{321}{123}，-321123\frac{321}{123}这样只有符号不一样的数，互为相反数（opposite number）。
就是说，1和-1互为相反数，1的相反数是-1，-1的相反数是1。
教材中说到：一般地，a和-a互为相反数。
其中，a表示任意一个数，包括正数，负数，甚至可以是0。举个例子，当a=2时，-a=-2，2的相反数是-2。当然，a也可以为-2。
值得一提的是，0的相反数就是0。
其实很容易看出，在a前面加上负号就是它对应的相反数了！
当a为负数时，如a=-4，在前面加上负号后表达为-（-4），即等于4。就是人们常说的负负得正。
当a为0，则表达为-0=0。
可以知道，-a不一定是负数（易错）。
大家可以尝试在数轴上表示一下相反数，看看有什么关系。

1.3.2 绝对值

10与-10互为相反数，在数轴上用A,B分别表示则是图1.3-1的样子。
图1.3-1
可以发现，A,B到原点的距离都是10。
为了描述这个距离，数学家们提出了绝对值（absolute value），并将这个距离命名为绝对值。

回归教材
一般地，数轴上表示数a的点与原点的距离叫做数a的绝对值。

绝对值记作∣a∣|a|，例如图1.3-1中，A,B两点到原点的距离都是10，因此10和-10绝对值都是10。记作：
∣10∣|10|=10，∣−10∣|-10|=10。
值得一提的是，0的绝对值是0。
那么，我们可以直接得到一个结论：
一个正数的绝对值是它的本身；一个负数的绝对值是它的相反数；0的绝对值是0。
在一些题目中，可能会问几个数中，绝对值最大或最小的数是什么。我们通过一个例题来看看。

例题3-1
如图1.3-2，数轴上的点A,B,C,D分别表示有理数a,b,c,d，这四个数中，绝对值最小的是哪个数？
图1.3-2
解答
因为在点A,B,C,D中，点C离原点最近，所以在有理数a，b，c，d中，c的绝对值最小。

怎么样，还挺简单的吧。

1.3.3 大小比较

小学我们已经知道两个正数或0的大小比较。那么有理数该怎么比较呢？
我们可以借助数轴来进行比较。
现在给你7个数：
-4，-3，-2，-1，0，1，2。
将这七个数放在数轴上表示，就是图1.3-3的图像。
图1.3-3
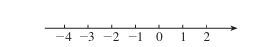
数学中规定：它们从左到右的顺序，就是从小到大的顺序。也就是说，左边的数小于右边的数。这里不一一列举。
我们通过教材上的例题了解这种题目该怎么写。

例题3-2
比较下面各组数的大小。
（1）5和-2；
（2）-3和-7；
（3）-（-1）和-（+2）；
（4）-（-0.5）和∣−1.5∣|-1.5|。
解答
（1）因为正数大于负数，所以5>-2。
（2）先求绝对值，分别是3和7。
因为3<7，即∣−3∣|-3|<∣−7∣|-7|。所以-3>-7。
（3）先化简，分别为1和-2。
因为正数大于负数，所以1>2。
即-（-1）>-（+2）。
（4）先化简，分别为0.5和1.5。
因为0.5<1.5。
所以-（-0.5）<∣−1.5∣|-1.5|。