更新记录
注意：仅作参考

2025-8-26

1.修改部分内容。
2.修改标签。
3.修改封面图。

上一节课我们学了负数，我们所接触到的数的范围变大了，因此，我们要为这个范围制定一个统称。

1.2.1 有理数

我们先来整理一下之前学过的数。
1，2，3，4，5…这些是正整数(positive integer)。-1，-2，-3，-4，-5…这些是负整数(negative integer)。以上两种数，我们统称为整数(integer)。
上面是一些很简单的数，现在我们上升一个等级。
12\frac{1}{2}，32\frac{3}{2}，321123\frac{321}{123}，3.2等这样的数，我们称之为正分数(positive score)。而-12\frac{1}{2}，-32\frac{3}{2}，-321123\frac{321}{123}，-3.2这样的数，我们称之为负分数(negative score）。上面两种数统称为分数（score）。

易错点
3.2，0.1这样的小数，可以写成分数形式，因此也可以当成分数。一般我们认为，所有小数都是分数，所有分数都是小数。
带百分号的数是分数（小数），如30%

而以上所有的数，我们统称为有理数（rational number）。在新人教版教材中，它的定义如下。

回归教材
有理数定义：可以写成分数形式的数称为有理数。

当然，有理数又被细分为正有理数和负有理数。这里不再过多介绍。大家可以自己做题练手。

1.2.2 数轴

我们来看人教教科书上的一个问题。

(摘自人教版教科书)问题导入
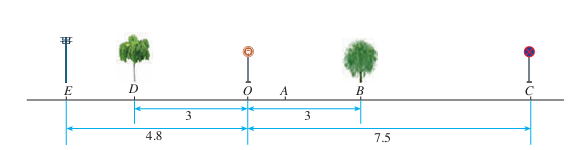
在一条东西向的马路旁，有一个汽车站牌，汽车站牌东侧3m和7.5m处分别有一棵柳树和一根交通标志杆，汽车站牌西侧3m和4.8m处分别有一棵槐树和一根电线杆，试画图表示这一情境。

(摘自人教版教科书)问题答案
如图1.2-1，画一条直线表示马路，从左到右表示从西到东的方向，在直线上任取一点O表示汽车站牌的位置，规定1个单位长度(线段OA的长度）代表1m长。于是，在点O右边，与点O距离3个和7.5个单位长度的点B和点C，分别表示柳树和交通标志杆的位置；在点O左边，与点O距离3个和
4.8个单位长度的点D和点E，分别表示槐树和电线杆的位置。
图1.2-1

上面的问题，我们可以抽象成一条直线，在O左边的记为负数，右边的记为正数。这个很好理解，给大家看一张教材的图片（图1.2-2）就可以理解了。
图1.2-2
这样就可以简单地表示出各种地点的相对位置关系了。
根据这个，我们就可以进一步的深入。
在数学中，我们可以用一条线上的点表示数，这条线就是传说中的数轴（Number axis）。
数轴可不是简单的一条线，它包含很多的元素，我们来讲一讲数轴的三个条件：
条件一：在直线上任取一个点，表示0，这个点也叫做原点（origin）。
条件二：一般地，我们规定从原点向右或向上为正方向，反之为负方向。
条件三：选取适当长度为单位长度，从原点向正方向，每隔一个单位长度画一个点，依次用1，2，3…表示；向负方向，每隔一个单位长度画一个点，依次用-1，-2，-3…表示。
你可能看得一头雾水，给你看张教材中的图片（图1.2-3），你可能就明白了。
图1.2-3

易错点
正方向末尾要标上箭头。

教材中规定，有原点、正方向和单位长度的直线叫作数轴。
有理数都可以用数轴上的点表示，例如，在正半轴上，距离原点3个单位长度的点表示数3；在负半轴上，距离原点2.1个单位长度的点表示数-2.1。
数轴对数学的发展起到了重要的作用。
在考试时，会让考生在数轴上表示数，我们来看书本上的一个例题。

例题2-1
画出数轴，并在数轴上表示下列的数：
3，-4，4，0.5，0，-52\frac{5}{2}，-1。
解答
如图1.2-4所示。
图1.2-4

感谢人教为我们提供的图片！